Cross-correlation
In signal processing, cross-correlation is a measure of similarity of two waveforms as a function of a time-lag applied to one of them. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long-duration signal for a shorter, known feature. It also has applications in pattern recognition, single particle analysis, electron tomographic averaging, cryptanalysis, and neurophysiology.
For continuous functions, f and g, the cross-correlation is defined as:
where f * denotes the complex conjugate of f.
Similarly, for discrete functions, the cross-correlation is defined as:
The cross-correlation is similar in nature to the convolution of two functions.
In an autocorrelation, which is the cross-correlation of a signal with itself, there will always be a peak at a lag of zero unless the signal is a trivial zero signal.
In probability theory and statistics, correlation is always used to include a standardising factor in such a way that correlations have values between −1 and +1, and the term cross-correlation is used for referring to the correlation corr(X, Y) between two random variables X and Y, while the "correlation" of a random vector X is considered to be the correlation matrix (matrix of correlations) between the scalar elements of X.
If  and
and  are two independent random variables with probability density functions f and g, respectively, then the probability density of the difference
are two independent random variables with probability density functions f and g, respectively, then the probability density of the difference 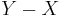 is formally given by the cross-correlation (in the signal-processing sense)
is formally given by the cross-correlation (in the signal-processing sense) 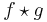 ; however this terminology is not used in probability and statistics. In contrast, the convolution
; however this terminology is not used in probability and statistics. In contrast, the convolution 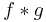 (equivalent to the cross-correlation of f(t) and g(−t) ) gives the probability density function of the sum
(equivalent to the cross-correlation of f(t) and g(−t) ) gives the probability density function of the sum 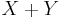 .
.
Contents |
Explanation
For example, consider two real valued functions  and
and  differing only by an unknown shift along the x-axis. One can use the cross-correlation to find how much
differing only by an unknown shift along the x-axis. One can use the cross-correlation to find how much  must be shifted along the x-axis to make it identical to
must be shifted along the x-axis to make it identical to  . The formula essentially slides the
. The formula essentially slides the  function along the x-axis, calculating the integral of their product at each position. When the functions match, the value of
function along the x-axis, calculating the integral of their product at each position. When the functions match, the value of 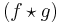 is maximized. This is because when peaks (positive areas) are aligned, they make a large contribution to the integral. Similarly, when troughs (negative areas) align, they also make a positive contribution to the integral because the product of two negative numbers is positive.
is maximized. This is because when peaks (positive areas) are aligned, they make a large contribution to the integral. Similarly, when troughs (negative areas) align, they also make a positive contribution to the integral because the product of two negative numbers is positive.
With complex-valued functions  and
and  , taking the conjugate of
, taking the conjugate of  ensures that aligned peaks (or aligned troughs) with imaginary components will contribute positively to the integral.
ensures that aligned peaks (or aligned troughs) with imaginary components will contribute positively to the integral.
In econometrics, lagged cross-correlation is sometimes referred to as cross-autocorrelation[1]
Properties
- The cross-correlation of functions f(t) and g(t) is equivalent to the convolution of f *(−t) and g(t). I.e.:
- If either f or g is Hermitian, then:
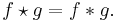
- Analogous to the convolution theorem, the cross-correlation satisfies:
where 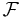 denotes the Fourier transform, and an asterisk again indicates the complex conjugate. Coupled with fast Fourier transform algorithms, this property is often exploited for the efficient numerical computation of cross-correlations. (see circular cross-correlation)
denotes the Fourier transform, and an asterisk again indicates the complex conjugate. Coupled with fast Fourier transform algorithms, this property is often exploited for the efficient numerical computation of cross-correlations. (see circular cross-correlation)
- The cross-correlation is related to the spectral density. (see Wiener–Khinchin theorem)
- The cross correlation of a convolution of f and h with a function g is the convolution of the correlation of f and g with the kernel h:
Normalized cross-correlation
For image-processing applications in which the brightness of the image and template can vary due to lighting and exposure conditions, the images can be first normalized. This is typically done at every step by subtracting the mean and dividing by the standard deviation. That is, the cross-correlation of a template, 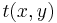 with a subimage
with a subimage 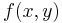 is
is
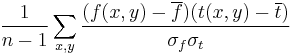 .
.
where  is the number of pixels in
is the number of pixels in 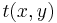 and
and 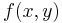 ,
, 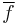 is the average of f and
is the average of f and 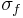 is standard deviation of f. In functional analysis terms, this can be thought of as the dot product of two normalized vectors. That is, if
is standard deviation of f. In functional analysis terms, this can be thought of as the dot product of two normalized vectors. That is, if
and
then the above sum is equal to
where 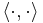 is the inner product and
is the inner product and  is the L² norm. Thus, if f and t are real matrices, their normalized cross-correlation equals the cosine of the angle between the unit vectors F and T, being thus 1 if and only if F equals T multiplied by a positive scalar.
is the L² norm. Thus, if f and t are real matrices, their normalized cross-correlation equals the cosine of the angle between the unit vectors F and T, being thus 1 if and only if F equals T multiplied by a positive scalar.
Normalized correlation is one of the methods used for template matching, a process used for finding incidences of a pattern or object within an image. It is in fact just the 2-dimensional version of Pearson product-moment correlation coefficient.
Time series analysis
In time series analysis, as applied in statistics, the cross correlation between two time series describes the normalized cross covariance function.
Let 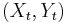 represent a pair of stochastic processes that are jointly wide sense stationary. Then the cross covariance is given by [2]
represent a pair of stochastic processes that are jointly wide sense stationary. Then the cross covariance is given by [2]
where 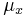 and
and 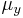 are the means of
are the means of 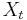 and
and 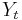 respectively.
respectively.
The cross correlation function 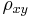 is the normalized cross-covariance function.
is the normalized cross-covariance function.
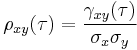
- where
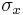 and
and 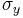 are the standard deviations of processes
are the standard deviations of processes 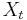 and
and 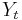 respectively.
respectively.
- where
Note that if 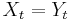 for all t, then the cross correlation function is simply the autocorrelation function.
for all t, then the cross correlation function is simply the autocorrelation function.
See also
- Autocorrelation
- Autocovariance
- Coherence (signal processing)
- Convolution
- Correlation
- Digital image correlation
- Phase correlation
- Spectral density
- Cross-spectrum
- Wiener–Khinchin theorem
References
- ^ Campbell, Lo, and MacKinlay 1996: The Econometrics of Financial Markets, NJ: Princeton University Press.
- ^ von Storch, H.; F. W Zwiers (2001). Statistical analysis in climate research. Cambridge Univ Pr. ISBN 0521012309.
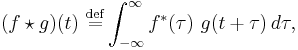
![(f \star g)[n]\ \stackrel{\mathrm{def}}{=} \sum_{m=-\infty}^{\infty} f^*[m]\ g[n%2Bm].](/2012-wikipedia_en_all_nopic_01_2012/I/7ebb1df08a4bbf572787a52b560dbfe9.png)
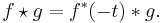

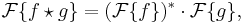
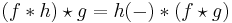
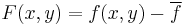
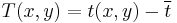
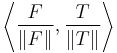
![\gamma_{xy}(\tau) = \operatorname{E}[(X_t - \mu_x)(Y_{t%2B\tau} - \mu_y)],](/2012-wikipedia_en_all_nopic_01_2012/I/d65b698d8d62c19ea287d7383b01e722.png)